Yes everyone, it's sad to say but this series is finally coming to an end. I decided to end it off as I don't want to drag it too long and also because I think 7 is a great number to end with. Lucky 7 you know?

Ok, so for today's problem we'll be looking at computing the Levenshtein distance (a.k.a. edit distance) between two words.

The Levenshtein distance (a.k.a. edit distance) between two words is the minimum number of single-character edits (insertions, deletions or substitutions) required to change one word into the other.

Given two words word1 and word2, find the minimum number of operations required to convert word1 to word2.

You have the following 3 operations permitted on a word:

Insert a character
Delete a character
Replace a character

Example 1:

Input: word1 = "horse", word2 = "ros"

Output: 3

Explanation:

horse -> rorse (replace 'h' with 'r')
rorse -> rose (remove 'r')
rose -> ros (remove 'e')

Example 2:

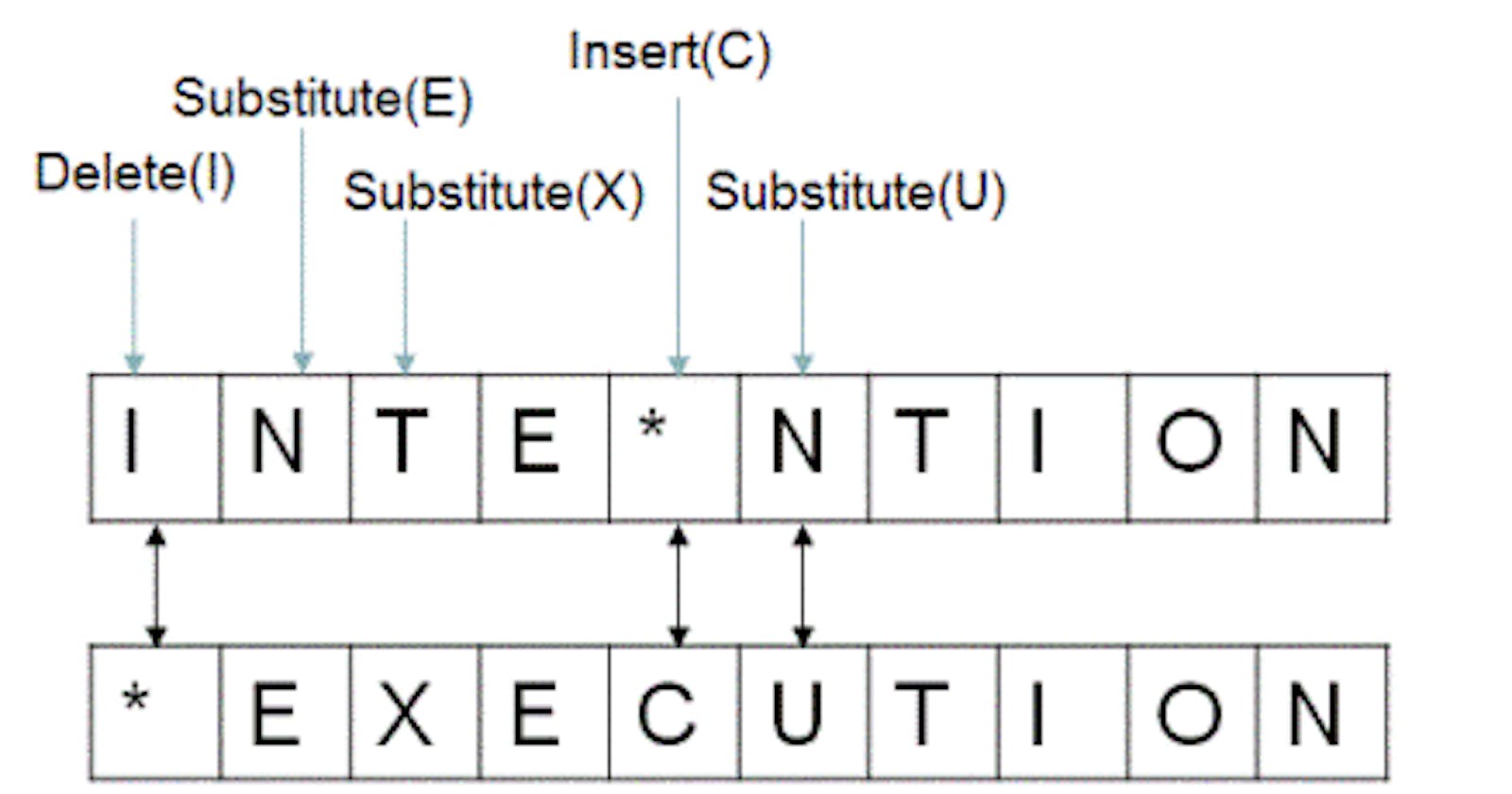
Input: word1 = "intention", word2 = "execution"

Output: 5

Explanation:

intention -> inention (remove 't')
inention -> enention (replace 'i' with 'e')
enention -> exention (replace 'n' with 'x')
exention -> exection (replace 'n' with 'c')
exection -> execution (insert 'u')

Our goal seems straightforward but as with most dynamic programming problems, building the foundation around the solution is the hardest.

I realize that I should mention this at the start of the series, but better late than never:

Dynamic programming problems applies well to problems which have the optimal substructure property: the optimal solution to the problem can be found given optimal solutions to subproblems, and we see this same property in divide-and-conquer type of problems as well. The difference is that in DP, subproblems overlap such that one subproblem require solution from another subproblem which makes memoization/tabulation great for reducing time complexity.

This just means that the key to solving any DP problem is to first try to break the main problem into a subproblem. Quite easily, we should see this:

Problem: Convert word1 to word2 by performing insert, delete, or replace operations on word1 (word2)

Subproblem: Convert word1[: i] to word2[: j] by performing insert, delete, or replace operations on word1

Now that we've broken down the problem, we'll need to establish the base case(s).

Base Case

Either word1 or word2 is an empty string

If word1 is an empty string, then we have to insert k number of characters into word1, where k = length of word2, so our cost here is k.
If word2 is an empty string, then we have to delete k number of characters from word1, where k = length of word1, so our cost here is also k

Data Structure and Tabulation

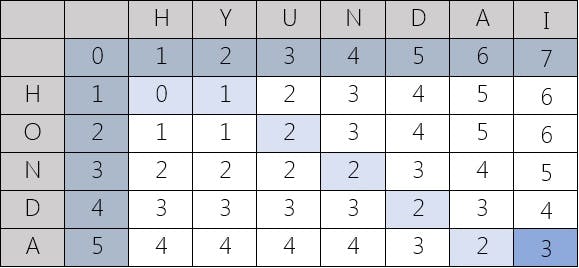
But now we need to store our base case somewhere, and what would be a good data structure to represent this? Well, when comparing two things, generally a matrix does it good right? One string can be on one axis and the other string can be on the second axis, and the value can be the Levenshtein distance between the two strings. For example, with HONDA and HYUNDAI we have:

Working Our Way Up

When working our way up, sometimes it can be useful to think about a recursive definition for our solution table. We know our base case, but are there what goes under our recursive case?

def lev_dist(word1, word2):
    n = len(word1)
    m = len(word2)
    if n == 0 or m == 0:
        return max(n, m)
    else:
        return ?

Note the value of n and m. By zero indexing, this means we have a matrix of (n+1) * (m+1). This is because we want to include the case of empty strings (i.e., dist_table[i][0] signals an empty string instead of the first letter of word2 and similarly, dist_table[0][j] signals an empty string for word1 instead of its first letter)

First, we need to ask ourselves when does it cost an operation to go from word1 to word2 and when does it not?

Case A: No cost This one is quite straightforward: the only way that no cost is required is when letters are the same. By recursive definition, this means:

Note: Python slicing works so that word[:k] is a substring of word from index 0 to index k-1, so index k is not included.

# if the last letters are the same
if word1[n] == word[m]:
    return lev_dist(word1[:n], word2[:m])

So we simply recurse on the substring excluding the last index.

Case B: When there is a cost Obviously, there is a cost if letters are different, so the opposite of Case A is essentially Case B. Let's break it down further into what operations can be done when the letters are different and how does it exactly affect our recursive definition.

Insert: this increases the length of word1 by 1 as we insert the last letter of word2 into word1 such that word1 and word2 now has the same last letters. Now, we can recurse on these strings like how we did in Case A by excluding the two letters that are the same, which will look like:
```
return lev_dist(word1, word2[:m]) + 1
```
Notice how we added 1 for an insert operation and that word1 essentially stays the same.
Delete: this reduces the length of word1 by 1, and we can simply recurse like so:
```
return lev_dist(word1[:n], word2) + 1
```
Replace: this replaces the last letter of word1 into the same letter as word2's last letter so that Case A applies and we can recurse similarly:
```
return lev_dist(word1[:n], word[:m]) + 1
```

Putting this all together, we now have our final recursive definition:

def lev_dist(word1, word2):
    n = len(word1)
    m = len(word2)
    if n == 0 or m == 0:
        return max(n, m)
    else:
        if word1[n] == word[m]:
            return lev_dist(word1[:n], word2[:m])
        else:
            return 1 + min(lev_dist(word1, word2[:m]),
                                    lev_dist(word1[:n], word2),
                                    lev_dist(word1[:n], word[:m]))

All that's left to do now is to convert this same idea into a bottom-up approach:

def bottom_up(word1, word2):
    dist_table = [[0 for i in range(len(word2) + 1)] for j in range(len(word1) + 1)]

    for i in range(1, len(word1) + 1):
        dist_table[i][0] = i  # base case

    for j in range(1, len(word2) + 1):
        dist_table[0][j] = j  # base case

    for i in range(1, len(word1) + 1):
        for j in range(1, len(word2) + 1):
            if word1[i-1] == word2[j-1]:
                dist_table[i][j] = dist_table[i-1][j-1]
            else:
                dist_table[i][j] = 1 + min(dist_table[i-1][j],
                                           dist_table[i][j-1],
                                           dist_table[i-1][j-1])

    return dist_table[len(word1)][len(word2)]

And this bring us to the end of the Dynamic Programming Series! Hopefully from this series, you have learned a lot on how to approach DP problems and and how to go about solving them so that you can ace your next interview! Good luck and thanks for reading!

Dynamic Programming Series #7 (Finale): Levenshtein Distance

Base Case

Data Structure and Tabulation

Working Our Way Up