Today's problem is definitely challenging, although it is quite a classic problem that you might have seen in your algorithms courses. For those of you who have seen this before, this will serve as a great comprehensive review, and for those who haven't seen this before, take your time to digest everything you'll learn here.
First, let's take a look at the problem.
We have n jobs, where every job is scheduled to be done from startTime[i] to endTime[i], obtaining a profit of profit[i].
You're given the startTime , endTime and profit arrays, you need to output the maximum profit you can take such that there are no 2 jobs in the subset with overlapping time range.
If you choose a job that ends at time x you will be able to start another job that starts at time x.
Example 1:

Input: startTime = [1,2,3,3], endTime = [3,4,5,6], profit = [50,10,40,70]
Output: 120
Explanation: The subset chosen is the first and fourth job.
Time range [1-3]+[3-6] , we get profit of 120 = 50 + 70.
Example 2:
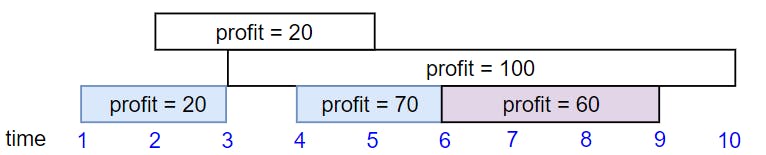
Input: startTime = [1,2,3,4,6], endTime = [3,5,10,6,9], profit = [20,20,100,70,60]
Output: 150
Explanation: The subset chosen is the first, fourth and fifth job.
Profit obtained 150 = 20 + 70 + 60.
Example 3:

Input: startTime = [1,1,1], endTime = [2,3,4], profit = [5,6,4]
Output: 6
Before we get into the solving this problem, let's consider a simpler version of this problem. Let's suppose that the profit for all jobs are equal. Essentially, what this means is that completing as much jobs as possible will be our optimal solution (it really doesn't matter what job you take as long as it is a job). Doesn't this sound familiar? Bingo! This sounds like a greedy algorithm type of problem.
Our greedy algorithm template:
- Consider jobs is some order
- Take each job if it doesn't conflict with the ones already taken
The key here is to determine the order we want to consider the jobs. Some orders we can consider...
- Shortest Interval: ascending order of (finish - start) times
- Fewest Conflicts: ascending order of Ci, where Ci is the number of remaining jobs that conflict with job i
- Earliest Start Time (EST): ascending order of start times
- Earliest Finish Time (EFT): ascending order of finish times
Let's consider each ordering and try to think of some counterexamples for them (i.e., why the order doesn't work).
Shortest Interval
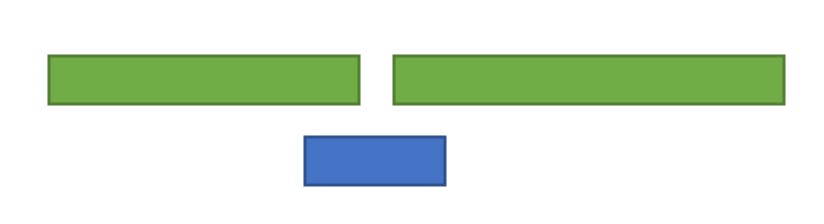
Fewest Conflicts

Earliest Start Time
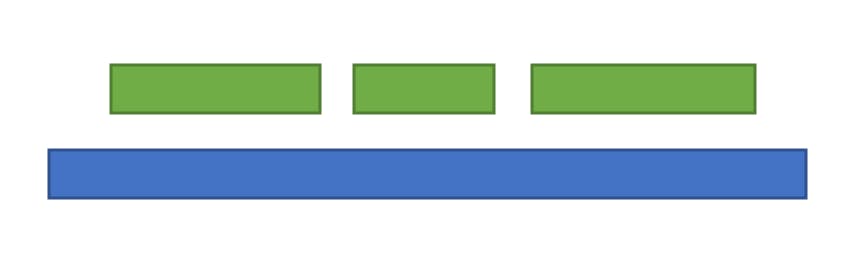
The blue bar indicates the job that the greedy algorithm will choose and for all the three cases, the solution is not optimal.
Finalizing our greedy algorithm with EFT
- Sort jobs in ascending order of finishing times
- When deciding whether job i should be included, check whether it conflicts with all previously added jobs by checking if start time of job i >= finish time of job i - 1
- If it doesn't conflict, then we can add it
Now, let's try to apply this greedy algorithm to our problem of maximizing profits in job scheduling when profits for each job are not the same. You'll realize that it will fail miserably. This is because now, not only is the number of jobs important, but also how much profit you make from the job. Which makes this a weighted interval scheduling problem, where each job is weighed differently such that the job with a higher profit is weighed higher than the job with a lower profit.
So what did we take away from the simple unweighted interval scheduling problem? Some nice insights but most importantly, the ordering that matters to us.
When jobs are unweighted, we can simply sort jobs in ascending order of finishing times and add the job if it doesn't conflict with previously added jobs. But in the weighted version, we should add if it doesn't conflict with previously added jobs AND increases our current profit. In other words, we want to take the max of (current profit + job i's profit, current profit). Using this idea, let's try to implement this in Python.
First, let's create a job class such that each instance of a job has a start time, an end time and a profit.
class Job:
def __init__(self, start, finish, profit):
self.start = start
self.finish = finish
self.profit = profit
Next, from our input arrays, let's create job instances and sort them based on their ending times like so:
def solution(startTime, endTime, profit) -> int:
jobs = []
for i in range(len(profit)):
jobs.append(Job(startTime[i], endTime[i], profit[i]))
# sort jobs in increasing order of their finish times
jobs.sort(key=lambda x: x.finish)
After that, doing our usual bottom-up approach:
# initialize max profit table
maxProfit = [0 for i in range(len(jobs))]
maxProfit[0] = jobs[0].profit
for i in range(1, len(jobs)):
# find the index of last non-conflicting job with current job
# j = -1 if no index could be found
j = get_last_non_conflicting_job(jobs, i)
# include the current job with its non-conflicting job
profit = jobs[i].profit
if j != -1:
profit += maxProfit[j]
# store the maximum profit by including or excluding the current job
maxProfit[i] = max(profit, maxProfit[i-1])
return maxProfit[len(jobs) - 1]
To get our last non-conflicting job, we can do a simple linear search.
def get_last_non_conflicting_job(jobs, n):
for i in reversed(range(n)):
if jobs[i].finish <= jobs[n].start:
return i
return -1 # if no non-conflicting job is found
Although, our linear search can be optimized further using a binary search instead.
def get_last_non_conflicting_job(jobs, n):
low = 0
high = n
while low <= high:
mid = (low + high) // 2
if jobs[mid].finish <= jobs[n].start:
if jobs[mid + 1].finish <= jobs[n].start:
low = mid + 1
else:
return mid
else:
high = mid - 1
return -1 # if no non-conflicting job is found
And we're done! I think the hardest part of this problem was realizing that ordering matters and determining the order in which we should iterate the jobs through, and that's why I focused on that. Besides that, it really is just another dynamic programming problem.
