Here is today's problem. Personally, I thought it was quite fun and just right in terms of difficulty.
A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below).
The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked 'Finish' in the diagram below).
How many possible unique paths are there?
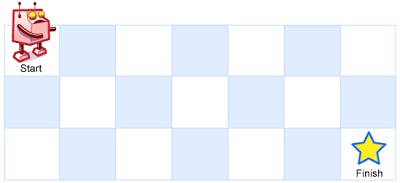
Above is a 7 x 3 grid. How many possible unique paths are there?
Example 1:
Input: m = 3, n = 2 Output: 3 Explanation: From the top-left corner, there are a total of 3 ways to reach the bottom-right corner:
- Right -> Right -> Down
- Right -> Down -> Right
- Down -> Right -> Right Example 2:
Input: m = 7, n = 3 Output: 28
Constraints: 1 <= m, n <= 100 It's guaranteed that the answer will be less than or equal to 2 * 10 ^ 9.
Like our previous problem, immediately we know that we should use the bottom-up approach to solve this problem since we are required to find ALL possible unique paths.
Base Case
In any bottom-up approach, we will need to first establish some base cases. For me, I think of base cases as cases that cannot be broken down further because they are the simplest form of a subproblem. Alternatively, if I can compute them in one step, independent of any previous results, then it must be a base case. Usually a good start to finding a base case is to look at the problem's smallest input size (i.e., an edge case). In our case, this would be m = 1 and n = 1. So how many unique paths if m = 1 and n = 1. It would just be 1.
Ok, so now we have established a base case. Are there any more?
Notice that a robot can only move down or right at any point in time, so this would mean that if m = 1, doesn't matter the value of n, there's only one unique path to get there. Similarly, if n = 1, doesn't matter the value of m, there's only one unique path. Wow, this base case is even more insightful than the first one we established! The first one we established is merely a subset of this base case!
Moral of the story: look for as many base cases as you can before trying to work your way up
Working Our Way Up
For cases where m > 1 or n > 1, how can we compute the possible unique paths from our base cases and previous results? Hopefully, this part is intuitive for you just like it has been for me. Because to me it was quite obvious that we can compute it from adding the solutions of two previous results: the possible unique paths coming from the left and the possible unique paths coming from the top.
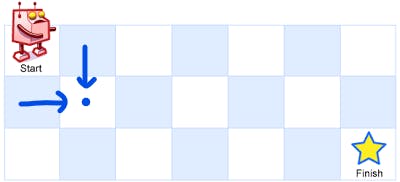
Essentially, solution[n][m] = solution[n-1][m] + solution[n][m-1] for all n, m > 1.
Implementation in Python
Now that we know what to do. Let's implement our solution in Python.
def main(m, n):
# initialization of solution table
solution_table = [[0 for i in range(m)] for j in range(n)]
# base case
# case 1: n = 1, only one way to traverse
for j in range(m):
solution_table[0][j] = 1
# case 2: m = 1, only one way to traverse
for i in range(n):
solution_table[i][0] = 1
for i in range(1, n):
for j in range(1, m):
solution_table[i][j] = solution_table[i-1][j] + solution_table[i][j-1]
return solution_table[n-1][m-1]
Great, we've finished our third dynamic programming problem! Do you think you're getting a hang of it?Cause I definitely feel like I am! In our next problem, I'll look at both ways (top-down and bottom-up) to solve a simple and classic problem in DP. Look forward to it!

